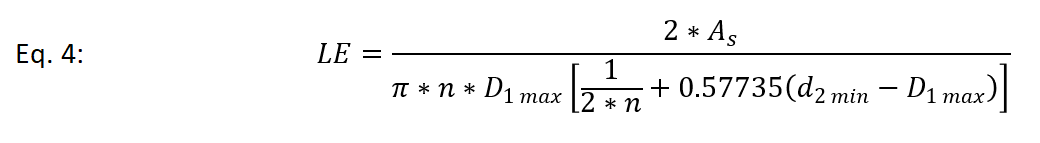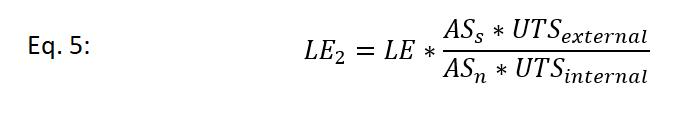How to Calculate Fastener Minimum Thread Engagement Length
Designing a bolted joint involves many structural considerations including preload requirements, torque requirements, thread engagements, etc. The bolted joint is expected to withstand the maximum applied forces to the joint over its lifetime of operations.
An important rule of thumb while designing bolted joints is to ensure that shear failure occurs in the screw or fastener, often times the externally threaded part. One of the few ways the designer of a bolted joint can control the strength of and failure point of the joint is with length of thread engagement. The length of thread engagement is the length of which the bolt and mating part’s threads are in contact with each other.
Keep in mind - While designing for minimum thread engagement length the designer should take into consideration the tolerance stack-up of the joint, the material ultimate tensile strengths, and the tapping tool being used.
Tensile Stress Area
The tensile stress area, or stressed area, is the cross-sectional area of the threaded part in direct contact with the mating threads. Threads are typically the weakest part of a bolt and most likely to be the cause of failure/fracture when in pure tension. Calculating and understanding the area of the bolt providing strength in tension will help in understanding how the thread engagement length can increase and decrease the strength of a joint.
The equation for the tensile stress area is:
Where:
A_s = Tensile shear area
d = Basic major diameter of external thread (in, mm)
n = # of threads per inch
Shear Area
Similar to the stressed area, the thread shear area is the cross-sectional area of the threads effective in resisting shear forces to the bolted joint. Shear failure in a bolted joint will look like thread stripping, and is “dependent, in addition, on mating component relative material strengths, nut geometry, and coefficient of friction between thread bearing surfaces.” [ASME B1.1-2003, Appendix B]
Where:
AS_s = Minimum thread shear area for external threads
AS_n = Minimum thread shear area for internal threads
n = # of threads per inch
LE = Length of thread engagement
d_1_min = Minimum major diameter of external thread
d_2_min = Minimum pitch diameter of external thread
D_1_max = Maximum minor diameter of internal thread
D_2_max = Maximum pitch diameter of internal thread
Minimum Thread Engagement
Generally, the minimum thread engagement length for a joint is determined such that the full tensile strength of the bolt is utilized prior to shearing of nut threads. In other words, it is expected that the shear failure occurs in the fastener part, often externally threaded, and the failure occurs only after utilizing full tensile strength.
Consider the formula below defining the minimum thread engagement length based upon shear of external thread. In this scenario, we assume both internally threaded and externally threaded parts are made of the same material with the same ultimate tensile strengths.
(variables defined above in equations 1 thru 3)
If the externally threaded part and internally threaded part have different material properties, specifically materially different ultimate tensile strengths, the thread engagement length will change to ensure the failure point is with the fastener. The thread engagement length is multiplied by a ratio of the shear areas and ultimate tensile strengths of the respective materials.
Where:
LE2 = Minimum thread engagement length (tensile strength and shear area ratio)
UTS_external = Ultimate tensile strength of external thread material
UTS_internal = Ultimate tensile strength of internal thread material
To recap,
If the internal and external threads are made from the same material or have similar shear strengths, use equation 4.
If the strength of the external thread materially exceeds that of the internal thread, use equation 5.
Jarrett Linowes
Mechanical Engineer
omniamfg@gmail.com
Did I miss anything you are interested in? Send me an email or comment below!